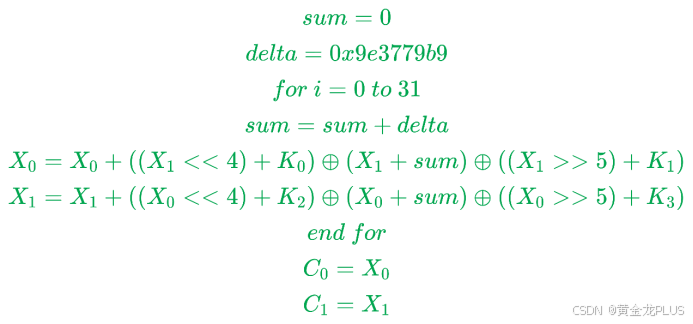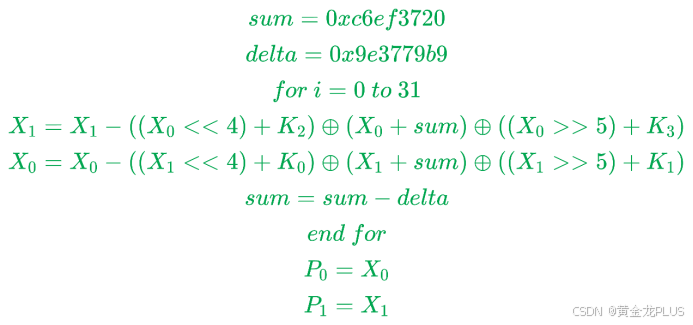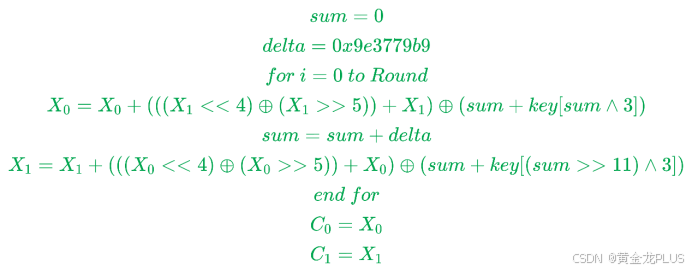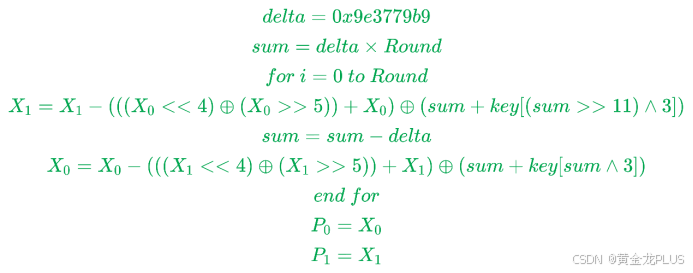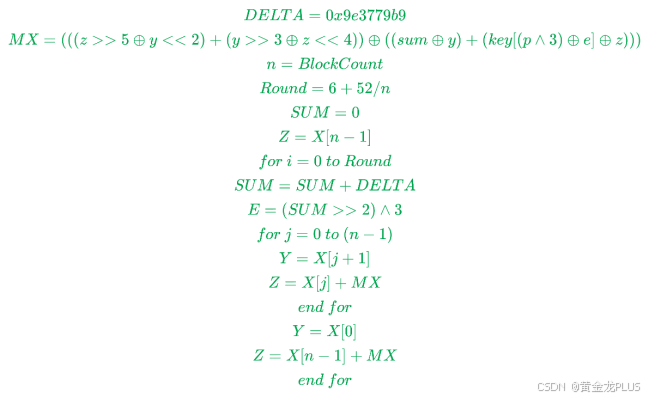TEA/XTEA/XXTEA系列算法

发表于 2025-12-20 更新于 2026-01-06 分类于 Reverse 本文字数： 2.3k

碰到了学一学。题啥的碰到了再补吧嗯嗯

引用：

https://bbs.kanxue.com/thread-266933-1.htm

https://www.cnblogs.com/zpchcbd/p/15974293.html （有借鉴上一篇

加解密工具：https://www.a.tools/Tool.php?Id=98（还有算法简介，抄了

https://blog.csdn.net/HuangJinLong2/article/details/145830787 （一顿偷图

有些细节搜不太到可能有总结错的地方

TEA（Tiny Encryption Algorithm）

1994年由英国剑桥大学的David j.wheeler发明

分组加密算法，实现非常简单，通常只需要很精短的几行代码。

TEA算法使用64位的明文分组和128位的密钥，它使用Feistel分组加密框架，Feistel需要进行64轮迭代，但是TEA作者认为32轮已经足够了，所以32轮迭代加密后最后得到64位密文。

该算法使用了一个神秘常数δ作为倍数，它来源于黄金比率，以保证每一轮加密都不相同。

推荐&默认值： δ=「(√5 - 1)231」，这个δ对应的数指就是0×9E3779B9

明文	每组8字节（64位bit）
密文	同明文
密钥	16字节（128位bit）
轮数	32（推荐）~64

加密

轮次：32轮

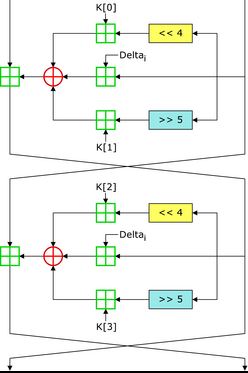
从图解中可以看到运算有加法运算，位运算，异或运算。

流程1：

1、首先TEA加密解密是以原文以8字节，所以从两边各自传入四个字节

2、右边传入的4个字节，这里将这4个字节称呼为M，M进行了三个部分的操作，M左移4位与密钥[0]相加，M右移5位与密钥[1]相加，M与δ相加，最后这三个算出的值再异或

3、左边传入的4个字节，这里将这4个字节称呼为N，N=N+M
流程2：

接着就到了下面这个部分，这里的话M和N交换了位置，

2、右边传入的4个字节，N进行了三个部分的操作，N左移4位与密钥[2]相加，N右移5位与密钥[3]相加，N与δ相加，最后这三个算出的值再异或

3、左边传入的4个字节，M=M+N

4、此时拿到的M和N就是加密过后的M和N

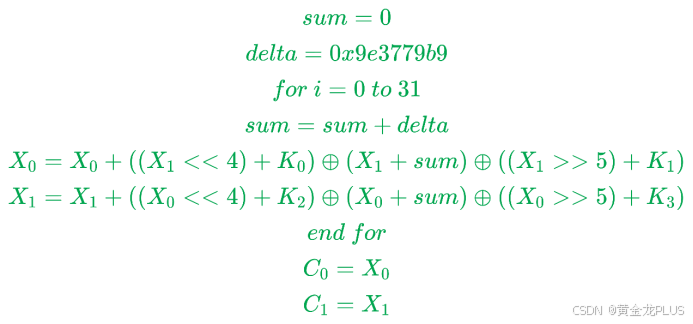
解密

解密就是

+=改为-= 左移位变右移位

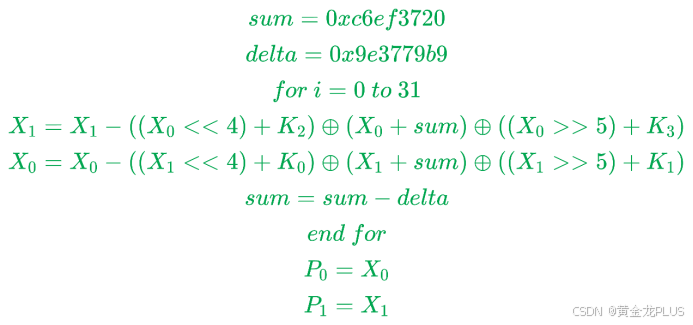
脚本

#include <stdio.h>
#include <stdint.h>
 
//加密函数
void encrypt (uint32_t* v, uint32_t* k) {
    uint32_t v0=v[0], v1=v[1], sum=0, i;           /* set up */
    uint32_t delta=0x9e3779b9;                     /* a key schedule constant */
    uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];   /* cache key */
    for (i=0; i < 32; i++) {                       /* basic cycle start */
        sum += delta;
        v0 += ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
        v1 += ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
    }                                              /* end cycle */
    v[0]=v0; v[1]=v1;
}
 
//解密函数
void decrypt (uint32_t* v, uint32_t* k) {
    uint32_t v0=v[0], v1=v[1], sum=0xC6EF3720, i;  /* set up */
    uint32_t delta=0x9e3779b9;                     /* a key schedule constant */
    uint32_t k0=k[0], k1=k[1], k2=k[2], k3=k[3];   /* cache key */
    for (i=0; i<32; i++) {                         /* basic cycle start */
        v1 -= ((v0<<4) + k2) ^ (v0 + sum) ^ ((v0>>5) + k3);
        v0 -= ((v1<<4) + k0) ^ (v1 + sum) ^ ((v1>>5) + k1);
        sum -= delta;
    }                                              /* end cycle */
    v[0]=v0; v[1]=v1;
}
 
int main()
{
    uint32_t v[2]={1,2},k[4]={2,2,3,4};
    // v为要加密的数据是两个32位无符号整数
    // k为加密解密密钥，为4个32位无符号整数，即密钥长度为128位
    printf("加密前原始数据：%u %u\n",v[0],v[1]);
    encrypt(v, k);
    printf("加密后的数据：%u %u\n",v[0],v[1]);
    decrypt(v, k);
    printf("解密后的数据：%u %u\n",v[0],v[1]);
    return 0;
}

逆向

1、tea算法的特征就是DELTA值和十六个字节的密钥（也就是128位）。

2、在逆向程序的时候，可以利用ida的插件findcypto识别tea算法

3、x-=0x61c88647和x+=0x9e3779b9，这两个值是等价的，都要注意

比如这个加密函数里就是是v10 -= 0x61C88647

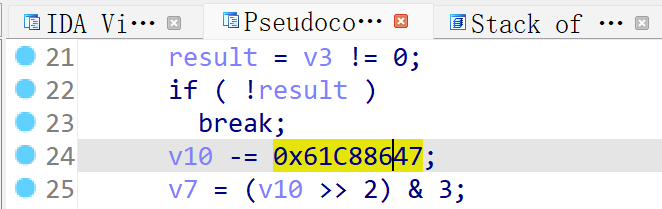
有可能点开汇编发现是+0x9e3779b9，不过这题汇编还是-0x61C88647哈哈

魔改

改变δ的值

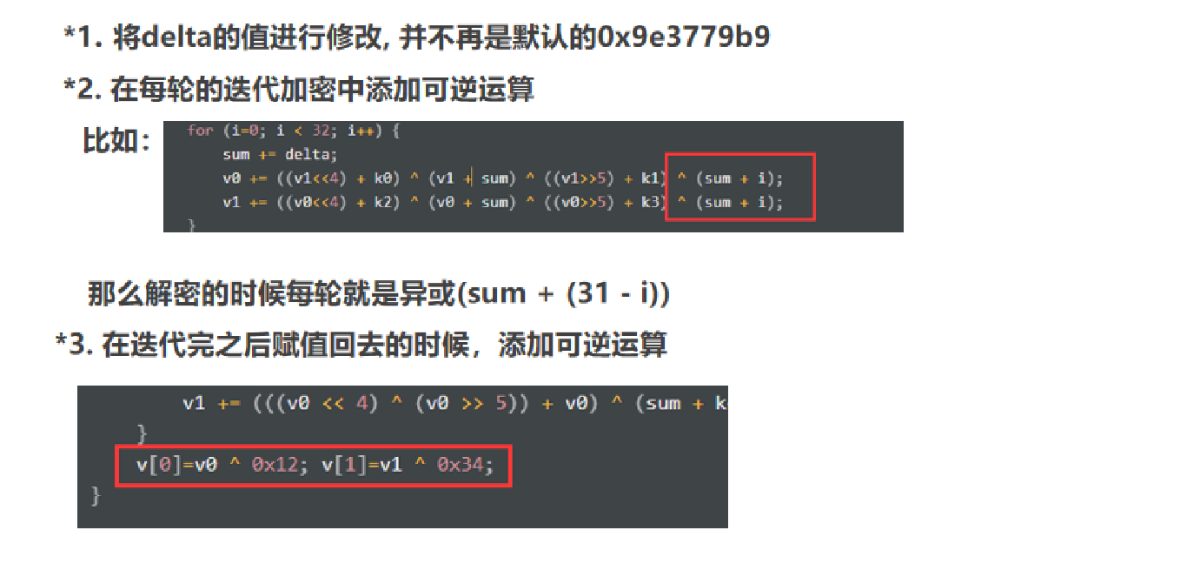
XTEA（eXtended TEA）

TEA的升级版，修补了 TEA 的密钥调度缺陷，增加了更多的密钥表，移位和异或操作等等，

设计者：Roger Needham, David Wheeler

TEA 算法被发现存在缺陷，作为回应，设计者提出了一个 TEA 的升级版本——XTEA（有时也被称为”tean”）。XTEA 跟 TEA 使用了相同的简单运算，但它采用了截然不同的顺序，为了阻止密钥表攻击，四个子密钥（在加密过程中，原 128 位的密钥被拆分为 4 个 32 位的子密钥）采用了一种不太正规的方式进行混合，但速度更慢了。

参数方面同TEA

加密

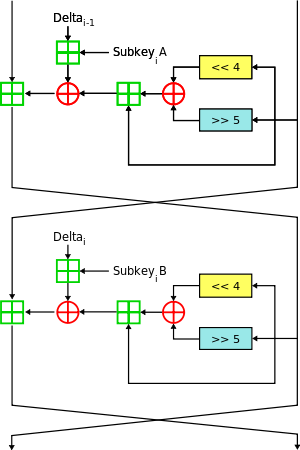
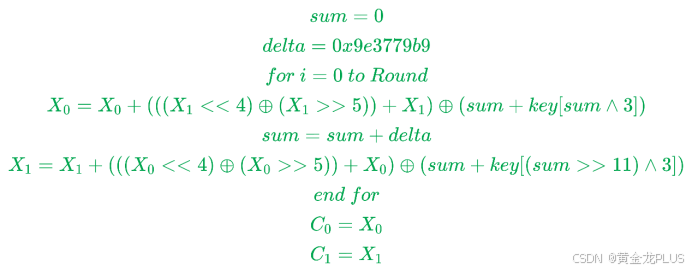
解密

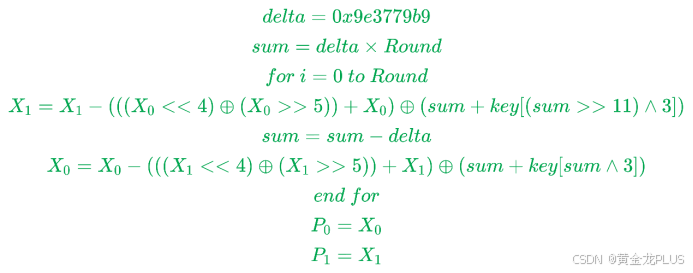
脚本

#include <stdio.h>
#include <stdint.h>
 
/* take 64 bits of data in v[0] and v[1] and 128 bits of key[0] - key[3] */
 
void encipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
    unsigned int i;
    uint32_t v0=v[0], v1=v[1], sum=0, delta=0x9E3779B9;
    for (i=0; i < num_rounds; i++) {
        v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
        sum += delta;
        v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
    }
    v[0]=v0; v[1]=v1;
}
 
void decipher(unsigned int num_rounds, uint32_t v[2], uint32_t const key[4]) {
    unsigned int i;
    uint32_t v0=v[0], v1=v[1], delta=0x9E3779B9, sum=delta*num_rounds;
    for (i=0; i < num_rounds; i++) {
        v1 -= (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[(sum>>11) & 3]);
        sum -= delta;
        v0 -= (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[sum & 3]);
    }
    v[0]=v0; v[1]=v1;
}
 
int main()
{
    uint32_t v[2]={1,2};
    uint32_t const k[4]={2,2,3,4};
    unsigned int r=32;//num_rounds建议取值为32
    // v为要加密的数据是两个32位无符号整数
    // k为加密解密密钥，为4个32位无符号整数，即密钥长度为128位
    printf("加密前原始数据：%u %u\n",v[0],v[1]);
    encipher(r, v, k);
    printf("加密后的数据：%u %u\n",v[0],v[1]);
    decipher(r, v, k);
    printf("解密后的数据：%u %u\n",v[0],v[1]);
    return 0;
}

XXTEA（Corrected eXtended TEA）

XTEA的升级版。有时也直接叫 Corrected Block TEA

设计者：Roger Needham, David Wheeler

Block TEA：Block TEA算法可以对32位任意整数倍长度的变量块进行加解密的操作，该算法将XTEA轮循函数一次应用于块中的每个字，并且将它附加于被应用字的邻字。

XTEEA使用跟Block TEA相似的结构，但在处理块中每个字时利用了相邻字，且用拥有两个输入量的MX函数代替了XTEA轮循函数。上面提到的相邻字实际上就是数组中相邻的项。

进一步把“逐 64 位块”扩展成“变长字块”，并修正了差分攻击弱点。

原字符串长度可以不是4的倍数了

明文	（每组）任意 4 字节（32bit）倍数	总长可以不是倍数，后面补0
密文	同明文	32bit的倍数
密钥	16字节（128位bit）
轮数	32（推荐）~64	默认`6 + 52 / n`

加密

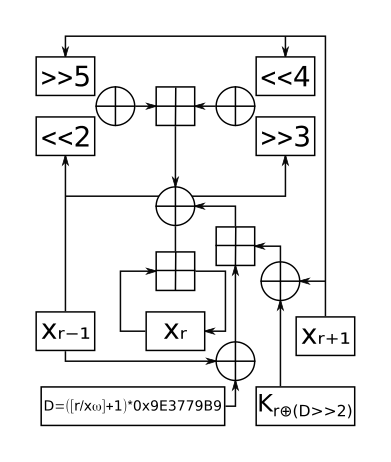
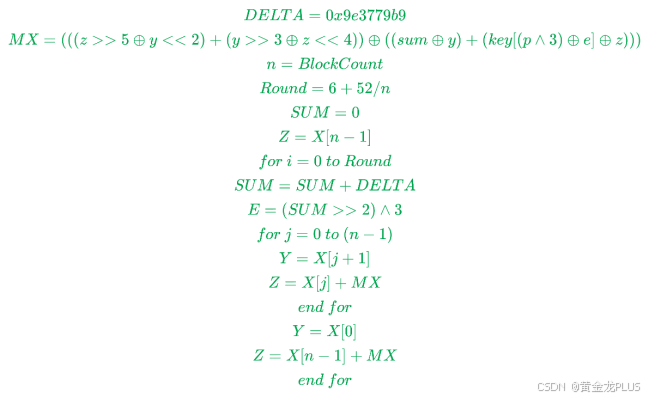
加密轮数：rounds = 6 + 52 / n，

https://blog.csdn.net/2301_80019887/article/details/154408267

这里我比较好奇为什么rounds = 6 + 52 / n，于是也搜集了一下加密轮数的设计原理：

保证最小安全轮数：基础轮数6是一个最小安全底线，即使数据块非常大，轮数也不会低于6轮，确保最基本的加密强度。

维持总操作量相对稳定：
1
总操作次数 = rounds * n = (6 + 52/n) * n = 6n + 52
52可以看作是一个固定的“开销”，而无论数据块大小如何，加密的总工作量大致是线性增长的。

小数据块需要更多轮数：当n很小时，数据块内部可供混合的”材料“有限；而大数据内部有更多的字可以相互影响，每一轮能达到更好的扩散效果。因此大数据块需要的轮数较少。

当然，这个公式中的52是一个经验值，取52时能在安全性和性能之间取得良好平衡。

解密

脚本

#include <cstdio>
#include <stdint.h>
#include <cstring>
#define DELTA 0x9e3779b9

static inline uint32_t MX_calc(uint32_t z, uint32_t y, uint32_t sum, const uint32_t key[4], unsigned p, unsigned e) {
    return (((z >> 5) ^ (y << 2)) + ((y >> 3) ^ (z << 4)))
           ^ ((sum ^ y) + (key[(p & 3) ^ e] ^ z));
}
/* 加密：out[] = encrypt of in[]  返回轮数，供解密用 */
void xxtea_encrypt(const uint32_t *in, int n, int rounds, const uint32_t key[4], uint32_t *out)
{
    uint32_t y, z, sum = 0;
    unsigned idx, cycle;

    memcpy(out, in, sizeof(uint32_t) * n);
    z = out[n - 1];

    while (rounds--) {
        sum += DELTA;
        cycle = (sum >> 2) & 3;

        for (idx = 0; idx < n - 1; idx++) {
            y = out[idx + 1];
            out[idx] += MX_calc(z, y, sum, key, idx, cycle);
            z = out[idx];
        }
        y = out[0];
        out[n - 1] += MX_calc(z, y, sum, key, n - 1, cycle) ;
        z = out[n - 1];
    }
}
/* 解密：out[] = decrypt of in[]  需要知道加密时的轮数（或再算一遍） */
void xxtea_decrypt(const uint32_t *in, int n, int rounds, const uint32_t key[4], uint32_t *out)
{
    uint32_t y, z, sum;
    unsigned idx, cycle;

    sum = rounds * DELTA;
    memcpy(out, in, sizeof(uint32_t) * n);
    y = out[0];

    while (rounds--) {
        cycle = (sum >> 2) & 3;

        for (int idx = n - 1; idx > 0; idx--) {
            z = out[idx - 1];
            out[idx] -= MX_calc(z, y, sum, key, idx, cycle);
            y = out[idx];
        }
        z = out[n - 1];
        out[0] -= MX_calc(z, y, sum, key, 0, cycle);
        y = out[0];
        sum -= DELTA;
    }
}

void print(uint32_t *data, int n){
    for(int i=0;i<n;i++){
        printf("%u ",data[i]);
    }
    printf("\n");
}

int main()
{
    uint32_t plaintext[2]= {1}; // plaintext为要加密的数据
    uint32_t ciphertext[2];
    uint32_t const key[4]= {2,2,3,4}; // key为加密解密密钥，为4个32位无符号整数，即密钥长度为128位
    int n = 1; 
    
    printf("加密前原始数据：");
    print(plaintext, n);
    xxtea_encrypt(plaintext, n, 6 + 52/n, key, ciphertext);
    printf("加密后的数据：");
    print(ciphertext, n);
    xxtea_decrypt(ciphertext, n, 6 + 52/n, key, plaintext);
    printf("解密后的数据：");
    print(plaintext, n);
    return 0;
}

题

可能可以看看那个1z_re